<
Previous
|
Next
|
Contents
>
Minkowski Mean
Minkowski mean is a generalization of arithmetic , quadratic and harmonic mean .
Minkowski mean is defined as
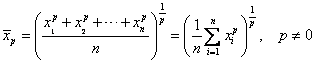
Example:
When
![]() , we have Arithmetic mean
, we have Arithmetic mean
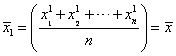
Example:
When
![]() , we have Harmonic mean
, we have Harmonic mean
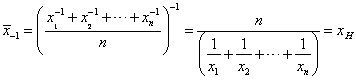
Example :
When p=2, we have Quadratic mean

However, we do not have a specific p in Minkowski mean to represent Geometric mean because Geometric mean is obtained through the limit of parameter p approaches 0, indicated by the formula below

Use the interactive program below to compute Harmonic mean of a list of numbers separated by comma. You may change with your own input values. Try to change the parameter p to a small number but not zero such as 0.0000000001 and compare the result with
Geometric Mean
.
Table below provides the summary of parameter to relate Minkowski generalized mean and other means.
|
Name |
Parameter p |
|
Arithmetic Mean |
p = 1 |
|
Geometric mean |
p approaches 0 (limit) |
|
Harmonic mean |
p = -1 |
| Quadratic mean | p = 2 |
< Previous | Next | Contents >
